Weighing the Universe
A public lecture given on Nov 4th 2019 as Visiting Professor of Cosmology at Gresham College, London. Part of a three lecture series in 2019-2020 on “The Nature of Reality”.
Surely you can’t “weigh” the Universe?!
Let us begin by clarifying the title of this lecture: “weighing” is not quite the right word. In fact, it is most definitely a physics mistake. “Weight” is a very confusing concept, and multiple definitions exists. Perhaps the one that is most familiar is that of the force exerted by gravity on a body. Alternatively, one could define “weight” as the force measured by the operation of keeping the object at rest in a gravitational field.
But this force depends on the gravitational field the body finds itself in. So, for example, I might weigh 60 kg on Earth[1], but I would weigh only 17% of that on the Moon, i.e. 10.2 kg, and two-and-a-half times more on Jupiter, i.e. 151.8 kg.
A more useful physical quantity is mass, which is the property of a physical body describing its resistance to acceleration. The mass of a body does not change in different gravitational fields (although it does change when moving at high speed, as a consequence of Einstein’s theory of special relativity). The equivalence principle formulated by Einstein says that the way a body responds to acceleration due to gravity is identical to the way it responds to acceleration due to any other force. In physics jargon, we say that the gravitational mass and the inertial mass are the same. One interesting and non-trivial consequence of this principle is that light also responds to gravity, even though the photon (the quantum of light) is massless – something that the Newtonian idea of gravity cannot explain.
So rather than “weighing the Universe” this lecture really is about measuring its mass. And here we immediately stumble on another conceptual problem: if the Universe is infinite (as modern cosmological data indicate), then surely its mass is infinite, too. What does it mean to measure it, then? We need a slightly more refined concept here, namely that of “mass density”, i.e., the average mass per cubic centimetre of space. This is a perfectly well-defined quantity: define a region of space (say, the entirely visible Universe), measure how much mass it contains, divide the total mass by the volume of the region in question et voilà, we have measured the average mass density of the visible Universe.
Gravity as geometry
Why would we want to measure the Universe’s mass density? Simply put, because the eventual fate of the Universe hangs in the balance, and the average mass density tells us whether the cosmos will continue expanding forever or whether it will recollapse onto itself in a Big Crunch. This is not quite the whole story, though, as we shall find out.
In order to understand how we can “weigh the Universe”, we need to go back to Einstein and to his revolutionary ideas about the nature of gravity. Einstein told us one hundred years ago that gravity is not a force, like Newton had said. Gravity is geometry.
Einstein unified space and time in a single entity, which he called “spacetime”. Spacetime is not rigid, but rather is dynamic and malleable: it reacts to the presence of mass by bending and changing its shape. In turn, masses (and even massless particles, such as photons, i.e., light) respond to the shape of spacetime by altering their trajectory. This is the deep insight into the nature of gravity that led Einstein to formulate his theory of General Relativity. It was such an incredibly different idea that it required exceptional observational confirmation, which came in 1919 when two teams of astronomers were sent by the Royal Astronomical Society to measure the apparent position of stars around the sun during a total solar eclipse. The observations were found to be in excellent agreement with Einstein’s predictions, thus validating his theory and propelling him to international stardom.
In 1929, Edwin Hubble determined that “nebulae” (which we now know were actually galaxies) are moving away from us with speed that is larger the further away they are[2]. This could be understood only if the Universe is expanding, an idea first proposed in 1927 by the Belgian priest and astronomer Georges Lemaître, building on Einstein’s theory of General Relativity. But if the Universe is expanding today, by winding back the cosmic movie we come to a point in the distant past when all of the visible Universe was concentrated in a point. This is what we now call “the Big Bang” (after the derogatory term coined by Fred Hoyle in the 1949), which Lemaître referred to as “the primordial egg”. The accidental discovery in 1965 of the cosmic microwave background (awarded the Nobel Prize for Physics in 1978[3]), the leftover radiation from the Big Bang, spectacularly confirmed this hypothesis.
The fate of the Universe
If the Universe has been expanding for the past 13.8 billion years, it is natural to ask the question as to whether it will continue to do so forever in the future. The answer depends on how much mass it contains. If the mass density (i.e., average mass per cubic centimetre) is sufficiently high, the gravitational attraction generated by that mass will eventually stop the expansion and reverse it: the Universe will end in a Big Crunch. If instead the mass density is not quite sufficient, then the Universe will continue to expand forever, at an ever decreasing speed.
However, there is a third, more exotic possibility. If in addition to gravity there existed a form of anti-gravity, then it is conceivable that the expansion of the Universe will not only continue forever, but will actually accelerate in the future. This implausible setup appears to be exactly what is realized in our Universe: the accelerated expansion of the cosmos was discovered in 1998 by two teams of astronomers, who used explosions of special stars, called supernovae type Ia, to measure the distance to galaxies and hence the rate of expansion. This unexpected discovery[4], whose authors won the Nobel Prize in Physics in 2011, demonstrated that there is more to the Universe than matter.
Precise measurements of the expansion history of the Universe have led to the conclusion that only about 5% of the matter-energy content of the cosmos is in the form of “normal” matter (i.e., the same sort of matter that makes up stars, planets, trees and people); 25% of the cosmos is made of dark matter (potentially a new type of elementary particle that we haven’t yet discovered in the lab) and a mighty 70% is made of dark energy – responsible for the accelerated expansion and possibly a manifestation of quantum fluctuations of empty space.
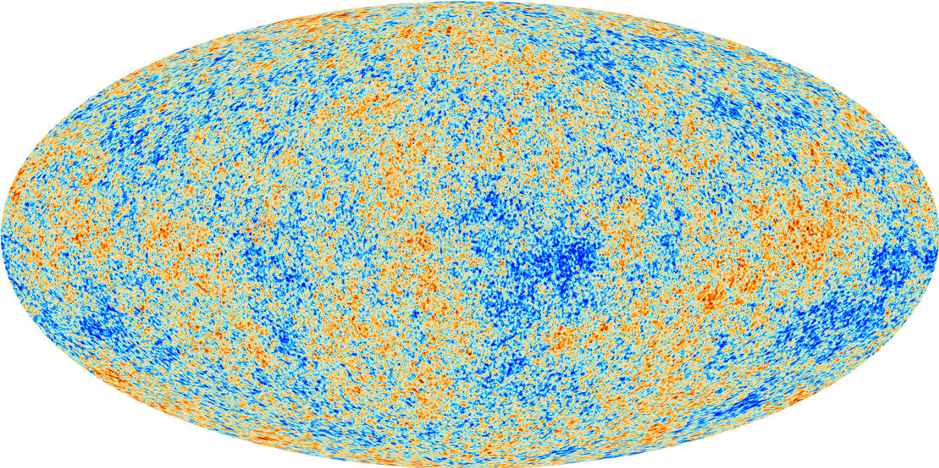
Cosmic sound
In 1994, the COBE satellite discovered the existence of tiny temperature imperfections in the cosmic microwave background. Since then, we have been able to map these ripples in the primordial Universe with greater and greater accuracy. The latest data from the Planck satellite[5] give us an exquisitely precise snapshot of the distribution of light in the cosmos when it was a mere 380,000 years old – before stars, galaxy or planets had had the time to form (Figure 1). Such imperfections originate from quantum fluctuations at the very beginning of time, right after the Big Bang. They are important as they constitute the seeds out of which galaxies eventually grew – without such seeds, galaxies wouldn’t grow, stars wouldn’t exist and we wouldn’t be here today to study the cosmos! Indeed, their importance for our understanding of our place in the Universe has been highlighted by two Nobel Prizes, one in 2006 for the experimental discovery of the fluctuations, and most recently in 2019 (to James Peebles) for the theoretical work that went into predicting their properties.
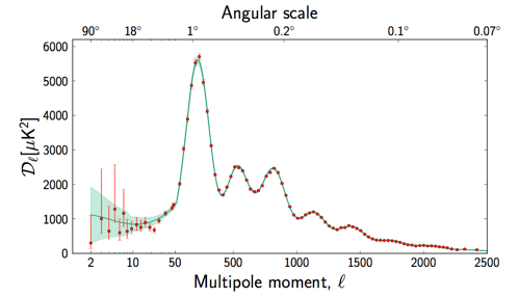
The statistical analysis of the fluctuations measured by the Planck space observatory reveals their underlying mathematical properties. When plotted in an appropriate manner, the fluctuations appear as a sinusoidal curve (Figure 2), which looks very much like a sound wave. This is not happenstance: the fluctuations themselves are the result of sound waves propagating at 60% of the speed of light in the hot plasma that permeated the Universe right after the Big Bang. These sounds were not meant to be heard by human ears: the base note has a wavelength of 450 million light years – to play it on a piano, you would need to extend its range by 78 octaves to the left! Nevertheless, this triumph of science (and music) rivals in beauty anything written by Bach.
The sounds waves of the baby Universe are useful to cosmologists as they give us the tool we need to “weigh the Universe” – or rather, to measure its average mass density. The idea goes as follows.
The shape of space
Three-dimensional space has three possible geometries: it can be flat (picture the surface of a table), open (like a saddle) or closed (like the surface of a sphere). In the first two cases, the spatial extent of the Universe is infinite, while in the third it is finite. The mass density of the Universe determines which of these three shapes it takes: open if the mass density is below a certain critical value; closed if it is above; and flat if it is just the critical value. By measuring the shape of the Universe we can infer its mass density – we will have “weighed it”.
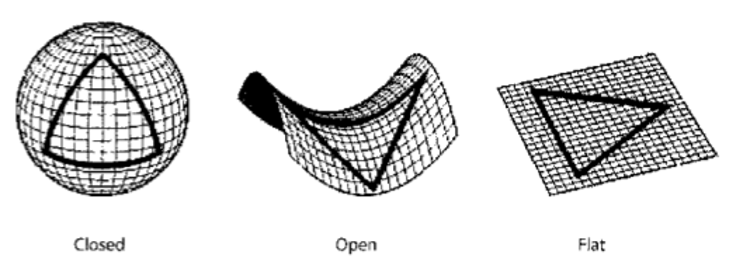
Of course we can’t measure the geometry of the Universe by “looking at it from the outside” – this works for the surface of the Earth, because it is a two-dimensional surface embedded in three-dimensional space. But since the Universe has three spatial dimensions, we have to find a way to measure its geometry without leaving it, which would impossible. Fortunately, there is a simple geometrical trick we can use, and that is to draw a big triangle and to look at the sum of its angles. Picture a triangle drawn on the flat surface of a table (Figure 3): Euclid tells us that the sum of its angles is exactly 180 degrees. But if the same triangle is drawn on the surface of a ball, the sum of its angles is more than 180 degrees. This is because the curvature of the sphere makes the angles “fatter”. Vice versa, draw the triangle on a saddle and the sum of its angles will be less than 180 degrees. What is more, we can do this experiment without ever leaving the surface of the table, or the sphere or the saddle. If we were beings confined to these two-dimensional surfaces, like ants, we would still be able to determine the kind of shape we are on without needed the benefit of seeing it “from above”.
We can do exactly the same experiment in our own Universe. Naturally, we need a very big triangle – one in fact that stretches all the way across the visible Universe. Fortunately for us, the sound waves in the baby Universe imprinted in the microwave background are just what we need: the distance between crests of the sound waves is known, and constitutes the short side of the triangle. The other two sides are the distance from us to each of the crests, traversed by the light beams that we have measured with Planck. We thus have a huge triangle that we can use to determine the geometry of the Universe.
And the answer is…
These measurements lead to the conclusion that the Universe is flat, with a margin of error of less than 1 per mille. This is in agreement with a prediction made by the theory of inflation: the very early Universe expanded very fast right after the Big Bang, thus smoothing out any curvature and making it indistinguishable from flat, exactly as we observe.
From this measurement we can also determine the average mass density, the quantity we have been after since the beginning of the lecture. The answer? Extremely small, namely: 0.000 000 000 000 000 000 000 000 000 003 837 grams per centimetre cube!
[1] This isn’t quite right, either, for weight is measured in newtons, the unit of measure for a force. For simplicity, let’s think of weight in this context as the number shown on a set of scales, usually displayed in kg.
[2] E. Hubble, “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae”, PNAS Volume 15, Issue 3, pp. 168-173 (1929).
[3] The Nobel Prize in Physics 1978, The Royal Swedish Academy of Sciences, Press Release, Oct 17th 1978, available from: https://www.nobelprize.org/prizes/physics/1978/summary/ (accessed: Oct 12th 2019).
[4] The Nobel Prize in Physics 2011, The Royal Swedish Academy of Sciences, Press Release, Oct 4th 2011, available from: https://www.nobelprize.org/prizes/physics/2011/summary/ (accessed: Oct 12th 2019).
[5] The Planck satellite mission: see https://sci.esa.int/web/planck (accessed Oct 12th 2019)
